Square ice Coulomb phase as a percolated vertex lattice

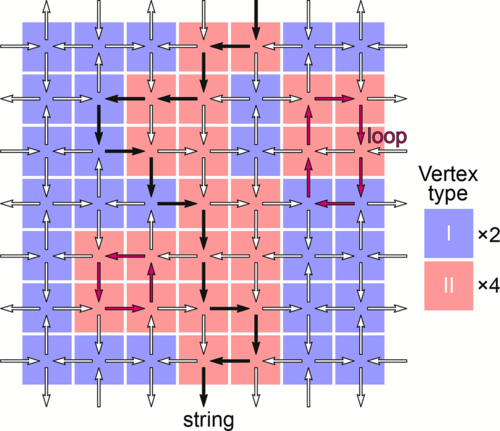
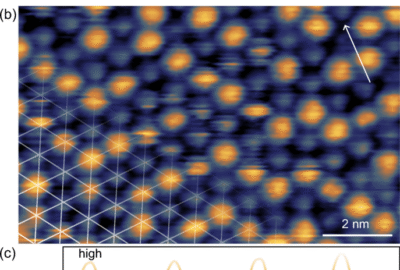
The square ice is a canonical example of a Coulomb phase in two dimensions: Its ground state is extensively degenerate and satisfies a local constraint on the spin arrangement (the so-called ice rule). In this paper, we use a loop flip algorithm to explore the properties of this ground state that we analyze not in terms of a spin texture, but rather in terms of a spatial distribution of ice-rule satisfying vertices. More specifically, we determine for various lattice sizes the average vertex populations characterizing the ice manifold, the pairwise vertex correlations, and the size distribution of vertex clusters. Comparing these results to those obtained from random, constraint-free vertex tilings, the square ice manifold is found to resemble an almost ideal vertex gas, and the cluster size distribution of ice-rule satisfying vertices is well approximated by percolation theory. Remarkably, this description remains reasonably accurate when monopoles are present in a dilute amount, allowing a direct comparison with experiments. Revising former experimental results on two artificial square ice systems, we illustrate the interest of our approach to spot the presence of a Coulomb phase from a vertex analysis.

J. Coraux, N. Rouger, B. Canals, and N. Rougemaille, Phys. Rev. B 2024, 109, 224422